Quadrilaterals
- Introduction to quadrilaterals, highlighting the distinction between irregular and symmetrical types, including trapezoids, parallelograms, rectangles, rhombuses, and squares.
- Explanation of fundamental properties common to all quadrilaterals, such as the sum of interior angles equating to 360 degrees and the presence of two diagonals.
- Detailed discussion on the 'big four' properties of parallelograms and how these properties are shared and extended in rhombuses, rectangles, and squares.
- Special focus on squares as elite quadrilaterals, emphasizing their unique position as having the properties of parallelograms, rectangles, and rhombuses.
- Insights into trapezoids, including the basic definition, properties, and the special case of symmetrical (isosceles) trapezoids.
Q: For the trapezoid ABCD practice problem, if we forget the 5-12-13 triangle rule, can we solve for the height another way?
A: Absolutely! That rule is just a shortcut - it's good to remember those, since they can save you time, but they're definitely not necessary to solve the problem.
Whenever we know two sides of a right triangle, we can just use the Pythagorean theorem to find the third side :) You can review that in this lesson: http://gre.magoosh.com/lessons/95-right-triangles
In the example here, we know that the hypotenuse is 13, and one of the other sides is 5. So we can just solve:
5^2 + b^2 = 13^2
25 + b^2 = 169
b^2 = 144
b = 12
So the height must equal 12.
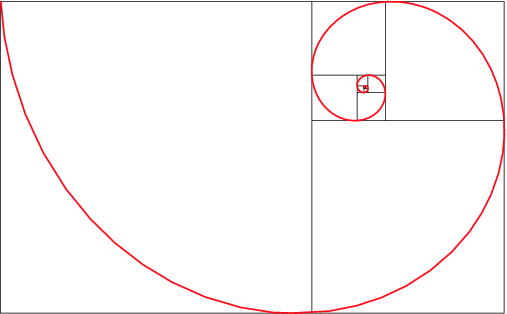
Q: So...what's a golden rectangle?
A: This definition from wikipedia is pretty good:
In geometry, a golden rectangle is a rectangle whose side lengths are in the golden ratio, which is 1:phi (that's the Greek letter phi), where phi is approximately 1.618.
Basically, it is considered a very pleasing rectangular figure with proportions that continue infinitely. It is also famous because if you continue splitting it into smaller pieces, you can form a spiral that is also pleasing. (See the image below.)
Now, to be clear, this concept isn't critical for your success on the GRE, but hopefully you found this interesting to learn :)