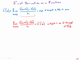Slope of Tangent
Next Lesson
Now that we've learned all this about limits, we're in a position to go back and talk about the solution to the problem of finding the slope to a tangent line. Suppose we have a function f of x and we want the slope of a tangent line at exactly one point, x equals a. Well, of course, we know it's easy to find the slope of a secant line. So suppose we go a small distance, h, over.
So, we're going between the points x equals h, x equals a, and x equals a plus h. And of course, the outputs at those functions, at those places, are gonna be f of a and f of a plus h. So the slope of the secant line is going to be the change in y, f of a plus h minus f of a, over the change in x, which is a plus h minus a.
Which is just h, that is the slope secant line. Now of course as we make h smaller and smaller, we get a secant line with the two points closer and closer together. That's going to approximate the tangent line, we can't actually plug in h equals 0 because then we would get a 0 over 0 limit, but now we know what we can do is, we can define it as a limit.
We can take the limit as h approaches zero of f of x plus h minus f of a over h. And this would give us the, the value of this limit, if it exists, would give us the slope of the tangent line. And in fact, this is something that we are defining and calling the first derivative. So, f prime of x, we read this as the first derivative of x of f of x.
And by f prime of a, we mean the slope of the tangent line to f of x, at x equals a. So this in fact, is the solution to the slope of the tangent line. In the next video, I will show an example of this.
Read full transcriptSo, we're going between the points x equals h, x equals a, and x equals a plus h. And of course, the outputs at those functions, at those places, are gonna be f of a and f of a plus h. So the slope of the secant line is going to be the change in y, f of a plus h minus f of a, over the change in x, which is a plus h minus a.
Which is just h, that is the slope secant line. Now of course as we make h smaller and smaller, we get a secant line with the two points closer and closer together. That's going to approximate the tangent line, we can't actually plug in h equals 0 because then we would get a 0 over 0 limit, but now we know what we can do is, we can define it as a limit.
We can take the limit as h approaches zero of f of x plus h minus f of a over h. And this would give us the, the value of this limit, if it exists, would give us the slope of the tangent line. And in fact, this is something that we are defining and calling the first derivative. So, f prime of x, we read this as the first derivative of x of f of x.
And by f prime of a, we mean the slope of the tangent line to f of x, at x equals a. So this in fact, is the solution to the slope of the tangent line. In the next video, I will show an example of this.