X vs T Slope
Next Lesson
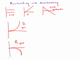
We'll begin our study of calculus by talking about graphs of distance versus time. These are graphs that are used in physics. So, imagine we have axis here. Now the vertical axis here is distance. You can think of this as a vertical number line and a point that moves back and forth along this line.
And then this axis is time. So as, say a bug or a dot, moves back and forth along this distance axis, as time goes on, it would trace out a shape. So a couple things to notice. First of all, let's just look at straight line graphs on this. Suppose I have a graph like this?
Well, what this would mean, a horizontal line, it would mean that we're at the same position. At all times. So, that would be something that was just sitting still. That would be something that would have a velocity of zero, and was just sitting there.
Now, meanwhile, suppose I have a graph like this? A straight line at an angle. Well, this is a line that, of course, has a slope. And of course, if you think about what slope is, slope is rise over run. Well, here the rise is a change in position over a change in time. Change in position over change in time, and in fact that is something we recognize as velocity.
So the slope on this graph equals the speed, or the velocity of the particle. Now that's very interesting. And, of course, if we have something rising as a line rising with a constant slope, what that represents is something moving at a constant velocity. And, of course, it makes sense if we go back to think about this one, the horizontal line, which has zero slope, has zero velocity.
So in the next video, we'll talk about what happens when slope changes.
Read full transcriptAnd then this axis is time. So as, say a bug or a dot, moves back and forth along this distance axis, as time goes on, it would trace out a shape. So a couple things to notice. First of all, let's just look at straight line graphs on this. Suppose I have a graph like this?
Well, what this would mean, a horizontal line, it would mean that we're at the same position. At all times. So, that would be something that was just sitting still. That would be something that would have a velocity of zero, and was just sitting there.
Now, meanwhile, suppose I have a graph like this? A straight line at an angle. Well, this is a line that, of course, has a slope. And of course, if you think about what slope is, slope is rise over run. Well, here the rise is a change in position over a change in time. Change in position over change in time, and in fact that is something we recognize as velocity.
So the slope on this graph equals the speed, or the velocity of the particle. Now that's very interesting. And, of course, if we have something rising as a line rising with a constant slope, what that represents is something moving at a constant velocity. And, of course, it makes sense if we go back to think about this one, the horizontal line, which has zero slope, has zero velocity.
So in the next video, we'll talk about what happens when slope changes.