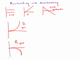
Accelerating and Decelerating
So we've already said, on a position versus timing graph that if we have a horizontal line, that is speed equal to zero, that's something just sitting still. If we have a line with a positive slope, that is something moving. Moving at a positive velocity. It's also true that we can have some we can have a line with a negative slope. And so this would be a velocity less than zero, which would mean that the object was moving backwards.
Well now with acceleration, we can throw in forward and backwards also. So for example, when we have a curve like this, a nice concave up curve. Well this is ordinary acceleration as we usually think about it, in other words, this is the car, in drive, and the person is stepping on the gas and the car is accelerating forward. But we might look at a curve that goes like this.
It's a notice what's happening, is that with this one, this concave down, and the slope is getting more or more negative, the absolute value of the slope is increasing. But it's pointing more and more in a negative direction. This would be if the person put the car in reverse. And then stepped on the gas.
So this is accelerating, backwards. We can also talk about, a curve that looks, like this. Well this is interesting. This starts out with a very, very high velocity, and then that velocity gets lower and lower.
And in fact, eventually goes to zero. So this is something that we typically would call, deceleration. Now, of course in physics we know that deceleration is a kind of acceleration, but this is called deceleration. And so this would be, the car is in drive but the person is stepping on the brake. And so velocity is decreasing and of course whenever velocity is changing, whether increases or decreases, that shows up on an X versus T graph as a curve.
Finally, we can have a curve that goes like this. So this was going, very negative, and then less and less negative, and down to zero, so this also was a deceleration, but this was a deceleration of a car that was moving backwards. So this is, deceleration backwards, in other words, the car is in reverse and the person is stepping on the brake.
And notice that, in the cases that are concave up, concave up, and that would be both, accelerating forward or decelerating backwards, in both of those concave up, the slope is increasing. In accelerating forward what's going on, is that we're starting with small positive values and moving to larger and larger positive values, we're decelerating backward.
We're starting with large negative values and then moving up to smaller and smaller negative values, eventually moving up to zero. So in both cases, we're moving up when we have a concave up graph. Similarly on the concave down graph, well, on this graph, we're moving from zero to bigger and bigger negative numbers. From this one, were moving from a positive number down to smaller and smaller positive numbers.
So on both cases on a concave down graph, what's happening is that the numbers for slope are decreasing. Those are usually important ideas which will come into play when we talk about the first and second derivative.
Read full transcriptWell now with acceleration, we can throw in forward and backwards also. So for example, when we have a curve like this, a nice concave up curve. Well this is ordinary acceleration as we usually think about it, in other words, this is the car, in drive, and the person is stepping on the gas and the car is accelerating forward. But we might look at a curve that goes like this.
It's a notice what's happening, is that with this one, this concave down, and the slope is getting more or more negative, the absolute value of the slope is increasing. But it's pointing more and more in a negative direction. This would be if the person put the car in reverse. And then stepped on the gas.
So this is accelerating, backwards. We can also talk about, a curve that looks, like this. Well this is interesting. This starts out with a very, very high velocity, and then that velocity gets lower and lower.
And in fact, eventually goes to zero. So this is something that we typically would call, deceleration. Now, of course in physics we know that deceleration is a kind of acceleration, but this is called deceleration. And so this would be, the car is in drive but the person is stepping on the brake. And so velocity is decreasing and of course whenever velocity is changing, whether increases or decreases, that shows up on an X versus T graph as a curve.
Finally, we can have a curve that goes like this. So this was going, very negative, and then less and less negative, and down to zero, so this also was a deceleration, but this was a deceleration of a car that was moving backwards. So this is, deceleration backwards, in other words, the car is in reverse and the person is stepping on the brake.
And notice that, in the cases that are concave up, concave up, and that would be both, accelerating forward or decelerating backwards, in both of those concave up, the slope is increasing. In accelerating forward what's going on, is that we're starting with small positive values and moving to larger and larger positive values, we're decelerating backward.
We're starting with large negative values and then moving up to smaller and smaller negative values, eventually moving up to zero. So in both cases, we're moving up when we have a concave up graph. Similarly on the concave down graph, well, on this graph, we're moving from zero to bigger and bigger negative numbers. From this one, were moving from a positive number down to smaller and smaller positive numbers.
So on both cases on a concave down graph, what's happening is that the numbers for slope are decreasing. Those are usually important ideas which will come into play when we talk about the first and second derivative.