Acceleration
Next Lesson
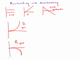
Changing slope on an X versus T graph. So suppose now we have our position axis and our time axis. And suppose we have motion of a particle that looks like this. Looks kind of like a parabola. Well what's going on with this kind of motion? Notice that, at some stages here, towards the beginning, the slope is lower.
And then the slope is getting higher and higher. So what's happening is that the slope is in fact increasing, unlike a straight line which has a constant slope, this is a curve that has an increasing slope. And what that would mean in terms of the particle was that speed is increasing. And of course, when speed is increasing the word we use for that is acceleration. So acceleration is represented by a curved line in a position versus time graph.
As opposed to constant velocity which is represented by a straight line. Notice also, one of the properties we can talk about the curve, the curve has what we call concavity. You may remember that convex or things that are pointing out in concave are pointing in. So for example, this is a lens that would be concave on both sides.
It is, it is curved inward on both sides. And so, this side of the graph has concavity and of course this side of the graph faces up. So we could call this a concave up graph. And that also is another way to describe acceleration. That's another way to describe the condition of the slope increasing.
Or the speed increasing. So acceleration is represented by a curved line, a line that is concave up on a position versus time graph.
Read full transcriptAnd then the slope is getting higher and higher. So what's happening is that the slope is in fact increasing, unlike a straight line which has a constant slope, this is a curve that has an increasing slope. And what that would mean in terms of the particle was that speed is increasing. And of course, when speed is increasing the word we use for that is acceleration. So acceleration is represented by a curved line in a position versus time graph.
As opposed to constant velocity which is represented by a straight line. Notice also, one of the properties we can talk about the curve, the curve has what we call concavity. You may remember that convex or things that are pointing out in concave are pointing in. So for example, this is a lens that would be concave on both sides.
It is, it is curved inward on both sides. And so, this side of the graph has concavity and of course this side of the graph faces up. So we could call this a concave up graph. And that also is another way to describe acceleration. That's another way to describe the condition of the slope increasing.
Or the speed increasing. So acceleration is represented by a curved line, a line that is concave up on a position versus time graph.